Estruturas de repetição

1. Introdução
2. Laço do tipo while
- 2.1. Laço do tipo while em Python
  - 2.1.1. Alguns exemplos
3. Laço do tipo for
- 3.1. Range
4. Referências e outros materiais

1. Introdução

Considere o problema encontrar o maior valor inteiro entre três fornecidos pelo usuário. Uma possível implementação é a seguinte:

maior = int(input("Digite um valor: "))
aux = int(input("Digite um valor: "))
if aux > maior:
    maior = aux
aux = int(input("Digite um valor: "))
if aux > maior:
    maior = aux
print(f"Maior = {maior}")

(Outras implementações são possíveis, utilizando, por exemplo, a função max do Python).

Mas imagine que o usuário deseja digitar 10 valores, ou trata-se de uma lista com milhares, talvez milhões de valores. Simplesmente repetir a mesma estrutura por 10, milhares ou milhões de vezes não é parece muito divertido.

De fato, para esse tipo de situação podemos utilizar laços de repetição. Uma estrutura que permite a repetição da mesma sequência de passos (possivelmente com valores diferentes) até que uma determinada condição seja atingida.

Em termos gráficos, o fluxograma reprenta um algoritmo que utiliza um laço de repetição.

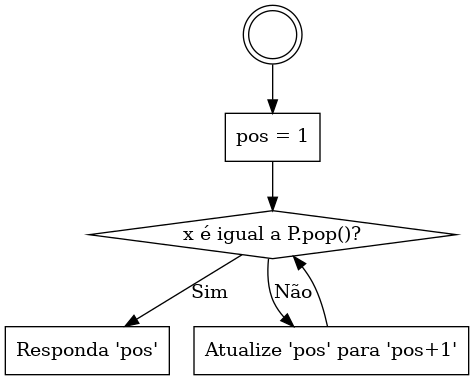
Em Python, há duas formas de implementar um laço de repetição, laços do tipo while e laços do tipo for. Discutidas na sequência.

2. Laço do tipo `while`

Considere o algoritmo de Euclides para encontrar o máximo divisor comum. Dados dois inteiros \(n\) e \(m\), \(m > n\), encontre o máximo divisor comum entre ambos da seguinte forma:

Seja \(r\) o resto da divisão de \(m\) por \(n\).
Se \(r = 0\), o algoritmo termina, \(n\) é a resposta.
Senão atualize \(m \leftarrow n\) e \(n \leftarrow r\) e volte ao passo 1.

Construa um fluxograma que representa o algoritmo de Euclides.

Em termos de pseudocódigo, podemos escrever o seguinte

leia (m, n)
r <- m % n
enquanto r != 0 faça
   m = n
   n = r
   r = m % n
imprima (n)

Note que o laço enquanto avalia uma condição booleana (True ou False). Caso a condição seja avaliada como verdadeira (True), então os comandos dentro do bloco while são executados. Após o comando r = m % n, reavalia-se a condição r!=0, caso ela seja verdadeira, repete-se os comandos do laço, caso contrário, o programa segue a partir do fim do laço (o comando imprima(n) neste caso). Cada repetição dos comandos do laço é chamada de iteração.

Em algoritmos iterativos, ao final de cada iteração é importante verificar o que deve ser feito para que a iteração seguinte inicie corretamente.

Para os valores \(m = 544\) e \(n = 119\), monte uma tabela com os valores de \(m\), \(n\) e \(r\) para cada iteração do laço.

2.1. Laço do tipo `while` em Python

Em Python, o laço while tem a seguinte estrutura sintática.

while cond:
    instrucoes

O campo cond é uma expressão avaliada como True ou False. O algoritmo de Euclides apresentado anteriormente pode ser implementado da seguinte for em Python.

m = int(input("Digite m: "))
n = int(input("Digite n: "))
r = m % n
while r != 0:
    m = n
    n = r
    r = m % n 
print("mdc = ", n)

Modifique o algoritmo anterior para garantir o seu funcionamento seja correto caso \(m < n\).

2.1.1. Alguns exemplos

Considere que se deseja fazer um programa que lê números do usuário até que seja fornecido um número negativo. O programa deve imprimir o número de valores positivos fornecidos. Uma possibilidade de implementação é a seguinte.

value = int(input("Digite um valor: "))
count = 0
while value > 0:
    count = count + 1  # Contador
    value = int(input("Digite um valor: "))
print(f"Positivos = {count}")

Monte uma tabela para acompanhar o valor das variáveis count e value ao longo das iterações.

Considere que se deseja fazer um programa que calcula \(S = 1 + 2 + \ldots + n\), com \(n\) fornecido pelo usuário. Um programa que realiza todas as somas é dado a seguir.

n = int(input("Digite n: "))
acc = 0  # Inicia com o valor nulo da soma
i = 0  # Conta os elementos somados ate' o momento
while i <= n:
    acc = acc + i 
    i = i + 1
print(f"S = {acc}")

Monte uma tabela com o valor das variáveis i e acc ao longo das iterações do algoritmo. Note o significado delas em relação a soma pedida.

Para o mesmo problema, pode-se observar a propriedade comutativa da adição e alterar o código para o seguinte.

n = int(input("Digite n: "))
acc = 0  # Inicia com o valor nulo da soma
while n > 0:
   acc = acc + n 
   n = n - 1
print(f"S = {acc}")

Monte uma tabela com o valor das variáveis acc e n ao longo das iterações do algoritmo. Note o significado delas em relação a soma pedida.

Considere que se deseja fazer um programa que lê números inteiros do usuário até que seja fornecido o caracter 'n'. O programa deve imprimir o maior valor fornecido. Uma possibilidade de implementação é a seguinte. Considere que pelo menos um valor numérico será fornecido.

largest = int(input("Digite um valor: "))
aux = largest
while aux != 'n':
    aux = int(aux)
    if aux > largest:
        largest = aux
    aux = input("Digite um valor: ")
print(f"Maior = {largest}")

Monte uma tabela com o valor das variáveis aux e largest ao longo das iterações do algoritmo. Note o significado delas em relação a soma pedida.

3. Laço do tipo `for`

Laços do tipo for são uma alternativa aos laços do tipo while. São particularmente úteis quando as iterações seguem um padrão "linear" como, por exemplo, iterar sobre todos os valores de uma coleção, ou de intervalo, um a um, ou dois a dois, ou três a três, etc.

Como exemplo considere o pseudocódigo a seguir, para imprimir todos os números inteiros no intervalo \([1, 10)\).

para i = 1, 2, ..., 9 faça
   imprime (i)

Em Python, um código equivalente seria o seguinte.

for i in range(10):
    print(i)

Note que foi utilizada a função range,

3.1. Range

A função range é utilizada para gerar sequências que seguem um padrão de progressão aritmética. Em seu uso mais simples podemos utilizar range(n) para gerar a sequência \((0, 1, \ldots, n-1)\). Mas também é possível utilizá-la com dois ou três argumentos. Resumidamente, tem-se:

range(n): gera a sequência \((0, 1, \ldots, n-1)\).
range(start, end): gera a sequência \((start, start+1, \ldots, end-1)\).
range(start, end, step): gera a sequência \((start, start+step, start + 2*step, \ldots, start + m*step)\), em que \(m\) é o maior valor tal que \(start + m*step < end\)

Altere a função range do script a seguir para atender cada um dos itens.

for i in range(10):
    print(i)

O código deve imprimir todos os números inteiros no intervalo \([10, 20)\).
O código deve imprimir todos os números inteiros no intervalo \([10, 20]\).
O código deve imprimir todos os números pares no intervalo \([10, 20]\).
O código deve imprimir os números \(10, 9, 8, \ldots, 0\), nessa ordem.
O código deve imprimir os números \(-10, -9, -8, \ldots, -5\), nessa ordem.
O código deve imprimir os números \(-10, -11, -12, \ldots, -15\), nessa ordem.
O código não deve imprimir nada.

Como exemplo, considere que se deseja calcular a soma de todos os números no intervalo \([10, 20]\).

total = 10
for i in range(10, 21):
    total = total + i
print(f"Total = {total}")

Para calcular a soma de todos os números pares, há pelo menos duas alternativas. A primeira, e mais elegante (em Python) é alterar a chamada da função range para iterar apenas sobre os números pares.

total = 0
for i in range(10, 21, 2):
    total = total + i
print(f"Total = {total}")

A segunda é utilizar uma estrutura condicional para checar a paridade dos números.

total = 0
for i in range(10, 21):
    if (i % 2 == 0):
        total = total + i
print(f"Total = {total}")

Laços do tipo for também são bastante convenientes para iterar em cada elemento de listas e strings.

4. Referências e outros materiais

Knuth, Donald E. The Art of Computer Programming: Fundamental Algorithms, volume 1. Addison-Wesley Professional, 1997.

Estruturas de repetição

Table of Contents